近日，上海交通大学物理与天文学院许霄琰课题组在《自然·通讯》（Nature Communications）在线发表了题为“Entanglement Rényi negativity of interacting fermions from quantum Monte Carlo simulations”的研究论文。该研究巧妙地利用了费米部分转置保高斯态的特性，创新性地提出了一种通过量子蒙特卡洛方法计算相互作用费米系统Rényi negativity的途径。研究团队首次在两个典型的强关联晶格模型中计算并分析了Rényi negativity的温度依赖关系，并揭示了有限温度相变点附近Rényi negativity的超出面积律行为。这项工作为在大规模强关联体系中探索混态量子纠缠现象开辟了新的研究方向。

量子纠缠作为量子信息科学的核心概念，近年来为凝聚态物理研究提供了新的视角，催生了多体量子纠缠这一新兴交叉领域。在多体系统基态研究中，纠缠熵的有限尺寸标度行为已被广泛应用于刻画量子物相和量子临界性。然而，对于混态（如有限温度吉布斯态），纠缠测量需排除经典关联的干扰，因此需要使用混态纠缠度量，例如对数negativity。Rényi negativity作为对数negativity的变种，其地位类似于Rényi纠缠熵与冯诺依曼纠缠熵之间的关系。它已在玻色子系统中被广泛应用于混态纠缠的研究，这得益于其更易于实现量子蒙特卡洛抽样算法。相比之下，尽管对自由费米子体系negativity的研究已经取得了一定的成果，但对于相互作用费米子系统而言，长期缺乏高效的混态纠缠测量方法，这严重阻碍了人们对强关联物理中纠缠特性的深入理解和研究。

研究团队利用了Shinsei Ryu等人在2017年所提出的费米部分转置保持高斯态的高斯性的性质，将费米子系统的部分转置密度矩阵在路径积分表象下表示为了加权求和，进而可以使用行列式量子蒙特卡洛来对Rényi negativity进行抽样（见图1）。该想法与最初2013年Tarun Grover提出的Rényi纠缠熵算法类似，补全了使用量子蒙特卡洛计算纠缠的另一块拼图。

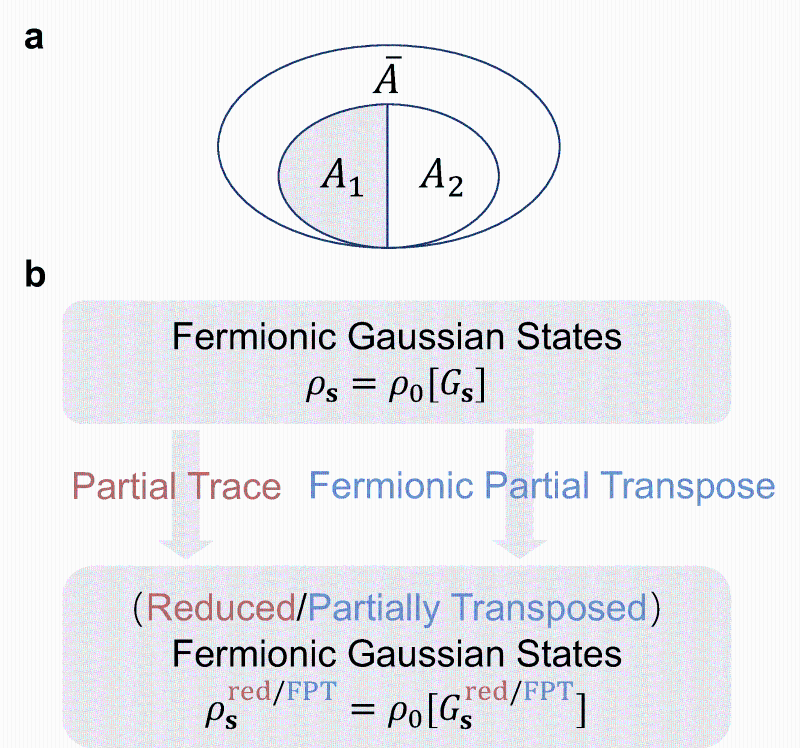
图1 （a）混态纠缠的三分几何示意图。在将环境（如无穷大固定温度热库）求迹之后，系统通常处于混态（如有限温度吉布斯态）。（b）高斯态的费米部分转置依然是高斯态，和部分求迹有着类似的行为。对辅助场s进行加权求和就得到了相互作用系统的部分转置密度矩阵，而这个加权求和可以在行列式量子蒙特卡洛框架下进行抽样。

作为该算法的应用实例，研究团队对一维Hubbard模型和正方晶格上的无自旋t-V模型进行了Rényi negativity温度依赖性的数值模拟。与Rényi纠缠熵随温度升高逐渐趋于体积律不同，一维Hubbard模型的Rényi negativity ratio表现出随温度单调递减的特征（如图2所示），这在定性上反映了从低温量子纠缠态到高温经典混合态的量子-经典交叉。更有趣的是，对于二维t-V模型，Rényi negativity ratio随温度升高呈现先上升后下降的趋势，并在有限温度相变点附近达到峰值（如图3所示）。此外，在相变点附近，Rényi negativity ratio的有限尺寸标度表现出超出面积律的行为，且在临界点上呈现L ln L的标度特性。这一现象与互信息在临界点处的交叉行为以及玻色子模型中Rényi negativity ratio随温度的单调递减趋势均存在显著差异。

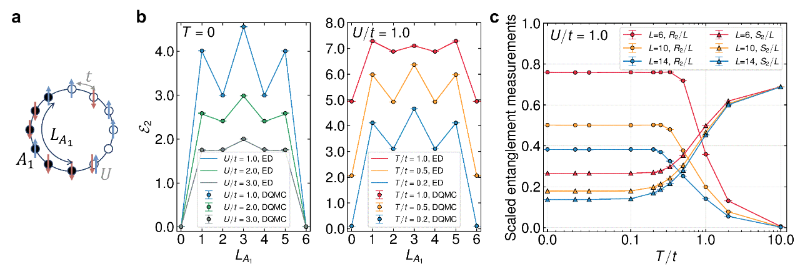
图2 （a）一维Hubbard模型和二分几何示意图。（b）不同温度和相互作用强度下，蒙特卡洛抽样结果和精确对角化结果的对比。（c）使用Rényi negativity ratio来揭示量子-经典交叉。

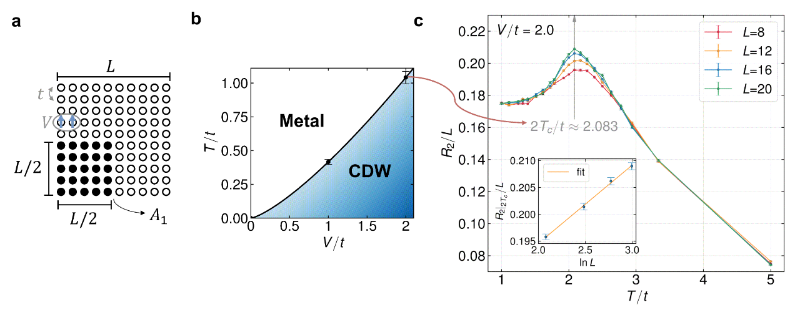
图3 （a）正方晶格上t-V模型和二分几何示意图。（b）使用Rényi negativity ratio探测的t-V模型相图。（c）不同尺寸下，Rényi negativity ratio的面积律系数随温度的变化关系。

该工作提出的方法具有广泛的适用性，可应用于多种量子蒙特卡洛框架，包括连续时间量子蒙特卡洛和限制路径-辅助场量子蒙特卡洛等。这为未来研究真实材料中的混态纠缠现象提供了新的契机。上海交通大学物理与天文学院博士生王佛泓为论文第一作者，许霄琰长聘教轨副教授为通讯作者。本工作主要由国家重点研发计划、国家自然科学基金、阳阳发展基金等项目资助，计算工作依托上海交通大学“思源一号”和“π2.0”超算平台完成，在此深表感谢。

论文链接：https://www.nature.com/articles/s41467-025-57971-8