近日，上海交通大学船舶海洋与建筑工程学院田新亮研究小组完成了“软尾减阻”的三维风洞实验，并发现了高达22.2%的减阻效果。该研究成果以“Drag reduction using a self-adaptive flexible coating”为题，在线发表在流体力学领域权威期刊《流体物理》（Physics of Fluids 36, 041701 (2024)），并被选为编辑精选文章。

2020年，该小组首次提出了为钝体穿“裙子”来减阻的方法（简称“软尾减阻”），即通过柔性薄膜包裹钝体使其“伪装”成流线体从而实现减阻 [1,2]。前期肥皂膜水洞实验证明了二维流场中最高约为10%的减阻效果。此后，国内外多个研究团队[3-5]及该小组[6,7]分别独立采用数值模拟方法，深入分析了二维场景下“软尾减阻”的物理机制和多种参数的影响。但是，该减阻方法能否用于实际工程，一直未获直接回答。

从2020年开始，研究小组在船海工程试验中心风洞循环水槽的支持下，逐步证明了 “软尾减阻”方法的工程实用性。首先在风洞实验室中构造了“软尾减阻”的三维实验模型，即“刚性平板+柔性薄膜”耦合系统。然后，建立了一套精密的测量系统（图1）：设计了悬挂系统释放约束来提升测力精度，开发了基于激光和高速摄像机的柔性薄膜高时空分辨率测量方法，研制了尾流烟线显示方法和装置。为了解决薄膜在大风中被吹瘪或吹破的问题，研究小组还提出了在平板正面开若干小孔来平衡薄膜内外压强的方法，不仅缓解了薄膜在风载作用下所受的张力，还使得薄膜在任何风速下均可达到鼓胀的效果。

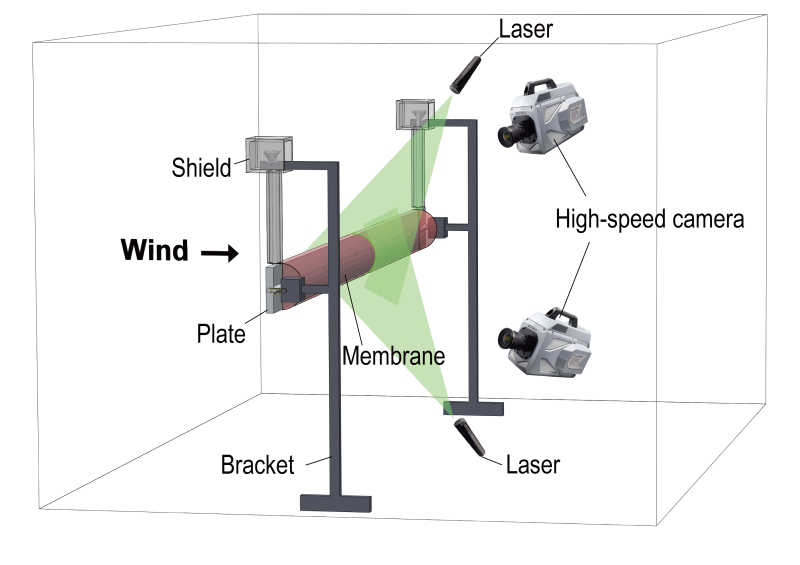
图1.三维风洞实验模型和测量装置示意图

实验表明，给一个三维平板“穿上”柔性薄膜“裙子”，减阻效果最高可达22.2%（见图2左）。值得注意的是，“裙子”的长度只有恰到好处才能减阻。如果穿得过长（>3.0）或者过短(<2.1)，不仅不会减阻，甚至会增阻。风洞实验中发现的最佳减阻软尾长度为2.4，与之前二维肥皂膜实验所得出的2.3非常接近，由此佐证了二维肥皂膜实验惊人的深层物理机制刻画能力。实验中发现，柔性薄膜可在风的作用下自然形成较为丰满的D型形态（见图2右），并伴随着泄涡过程在薄膜表面形成一种行波特征，以特定的频率和幅度抖动。这种自适应的薄膜形状和薄膜的拍动运动延迟了流动分离，显著减小了尾流宽度，从而降低了系统所受流体阻力（图3）。

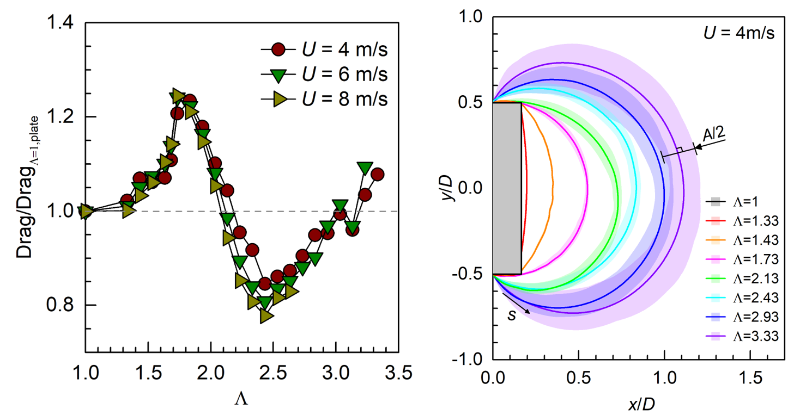
图2.平板所受阻力随薄膜尺寸的变化（左），时间平均的薄膜形状（右）

图3.平均尾流烟线图：（a）仅平板；（b）薄膜包裹的平板

风洞实验中的雷诺数最高达32000，达到了部分常见工程应用场景中的复杂流动的雷诺数。上述研究首次证明了“软尾减阻”在三维、高雷诺数、高湍流的流动条件下依然有效，为“软尾减阻”的工程应用潜力提供了最有力的直接证据。

船建学院博士研究生赵亚坤为论文第一作者，博士研究生张焕宇和孙姝悦分列论文第二和第三作者，船建学院船海试验中心彭涛正高级工程师和中船集团陈刚教授为论文合作者，田新亮教授为通讯作者。研究工作得到了海洋工程全国重点实验室、国家自然科学基金（U20A20328）、国家重点研发计划（2023YFC3107404）等项目支持。

论文链接：https://doi.org/10.1063/5.0204317

实验视频：https://pubs.aip.org/aip/pof/article/36/4/041701/3280713/Drag-reduction-using-a-self-adaptive-flexible

其他文献：

[1] S. Gao, S. Pan, H. Wang, and X. Tian, “Shape deformation and drag variation of a coupled rigid-flexible system in a flowing soap film,” Phys. Rev. Lett. 125, 034502 (2020).

[2] 田新亮. “软尾减阻”述评[J]. 上海交通大学学报, 55, 213-214 (2021).

[3] Q. Mao, Y. Zhao, J. Liu, and H. J. Sung, “Drag reduction by a flexible afterbody,” Phys. Fluids 33, 122009 (2021).

[4] Y. Sun, Z. R. Peng, D. Yang, Y. Xiong, L. Wang, and L. Wang, “Dynamics of a rigid-flexible coupling system in a uniform flow,” J. Fluid Mech. 943, A44 (2022).

[5] J. Y. Ni, W. X. Huang, and C. X. Xu, “Mode transition of a coupled rigid-flexible system in a uniform flow,” Phys. Fluids 35, 041706 (2023).

[6] H. Zhang, Y. Zhao, X. Tian, X. Wang, and H. Liu, “Symmetry breaking of a closed flexible filament behind a rigid plate at low Reynolds numbers,” Phys. Fluids 35, 024110 (2023).

[7] H. Zhang, Y. Zhao, X. Tian, and H. Liu, “Effects of the closed domain area on the dynamics of a closed flexible filament behind a rigid plate,” Ocean. Eng. 288, 115944 (2023).