全息对偶（简称“全息”）是25年前在弦理论背景下发现的重要理论工具。在自下而上的构造中，全息作为d+1维时空中弱耦合经典引力理论和d维时空中强耦合大N场论之间的对偶，为通往量子引力的非微扰构造打开了新的窗口，同时也为强耦合量子场论的研究提供了有效的方法。现如今，全息已经成为了一种补充性的并且高度跨学科的重要技术，被应用于包括凝聚态、流体力学、量子信息、非平衡物理、QCD等在内的许多研究领域。

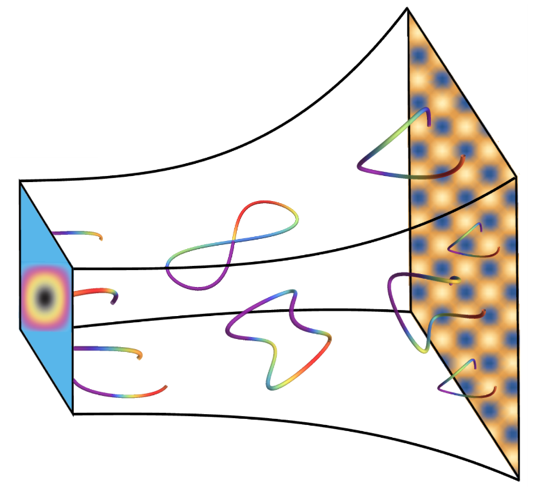
全息对偶的一个图示，将黑洞几何中引力的动力学映射到强耦合对偶场论的动力学。棋盘格结构表示对偶凝聚态体系中的平移序

在凝聚态方面的研究中，近年来重要的新进展都和利用各种方式在对偶场论中引入平移对称破缺有关。平移对称性破缺是描述凝聚态物质及其输运性质的基本要素，而这些研究的强烈动机来自于高温超导领域和奇异金属行为中尚未解决的问题。重要的是，这些发现为我们使用现代方式来理解粘弹性，以及构造有效理论来描述存在平移破缺的耗散系统带来了巨大的影响。全息方法不只是揭示了几个在流体力学和有效场论构造中缺失的部分，还为赝Goldstone模式的物理揭示了新颖的普适关系，这被后来更为标准的场论计算所证实和解释。

上海交通大学物理与天文学院的Matteo Baggioli教授和巴黎综合理工学院（École Polytechnique Paris）的Blaise Gouteraux教授在近期的研讨会上回顾了这些激动人心的发现，并且讨论了未来的主要研究方向和开放性问题，相关内容已经被发表在物理学领域最著名的综述期刊《现代物理评论》（Reviews of Modern Physics）上。

参考文献：

M.Baggioli and B.Gouteraux, “Colloquium: Hydrodynamics and holography of charge density wave phases”, Review of Modern Physics

论文链接：

https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.95.011001