
 综合新闻
综合新闻
2021年上海交通大学数学建模校内赛举行
首届上海交通大学数学建模校内赛于2021年8月20至24日举办,本次校内赛由教务处指导,学生创新中心和数学科学学院联合主办,上海交通大学人工智能创新创业基地、上海交通大学数学建模协会、上海卡方信息科技有限公司协办。赛事吸引了来自船舶海洋与建筑工程学院、机械与动力工程学院、电子信息与电气工程学院、数学科学学院、物理与天文学院、安泰经济与管理学院、交大密西根学院等20余个学院的近300位本科生和研究生报名参加。
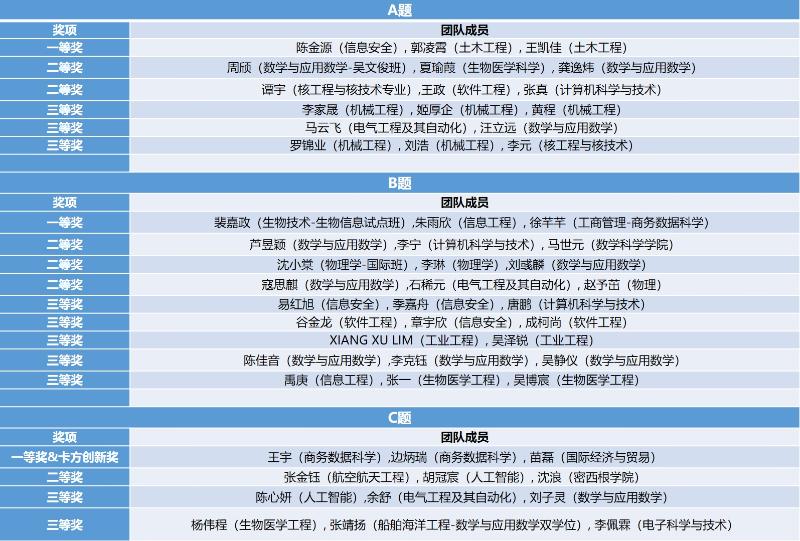
8月25日-9月7日,赛事专家组委会对正确提交的参赛论文,进行了分组评审,每一份论文均经由两名校内外专家打分,汇总后得到最终成绩,保证评审过程的客观、公正。经专家组委会评分,本次比赛的最终评审结果公示如下:
赛后点评
A题:双足步行
在本问题中,简化后的机器人步行可用二维倒立摆模拟。当作用于地面支撑点处的力矩为零时模型得到简化,整个体系只受到重力和直杆方向的地面支撑力f的作用。
问题1把模型进一步简化:倒立摆顶部的垂直高度保持不变,此时f需要满足一定的条件,支撑杆是有弹性的,它可伸缩。它的受力分析比较简单,大部分队伍能写出控制方程,并且给出了解析解。顶点A点的运动(位置和速度)依赖它的初始位置和初始速度,也依赖倒立摆的高度。很多小组都计算了倒立摆高度对A点运动的影响,部分优秀小组进一步分析了初始位置和初始速度对A点运动的影响,从而更能说明A点的运动规律,即:什么时候能顶点A能经过支撑点的垂直位置。
问题2是为从问题1过渡到问题3做准备的,分析的是支撑脚切换前后的位置和速度的描述。首先,在支撑过程中(问题1)轨道能量是守恒的。其次,切换前后的轨道能量是可变的。但是切换前后的位置和速度不变,它们应该保持连续性。最后,通过切换前后的轨道能量以及步长可确定切换时刻的位置和速度,大多数小组能够得到这个正确结论。但是,也有两个小组认为切换前后的轨道能量相同,这是不合理的。
问题3是需要对一步行走进行模拟,这需要对不同支撑脚支撑过程的模拟。注意,在支撑过程中的方程都是相同的,不同的是初始条件和速度和执行时间。最简单的一个假设是:假设所有轨道能量相同,比如有一个团队做了这样的模拟,并得到周期解,但是该论文没有讲清楚为什么是周期解。还有一个团队也在这个假设下进行模拟得到周期解,并且给出切换时刻的初始条件,这些周期解的结果是相对合理的。总的来说对问题3,虽然有些论文的模拟结果从图像上看比较合理,但对结果的分析还是不够细化。
问题4是对有(直线)斜坡时行走的模拟,顶点A的动力学和没有斜坡时的动力学方程相同(只要倒立摆的高度看成支撑点处斜坡方程的z坐标),有四个团队准确写出了这个微分方程,并基于问题3的求解方法进行了模拟,模拟结果都有一定的合理性。
问题5对顶点A不做任何限制。第一小问是对一般的支撑力f要模拟一个腿支撑在地面时顶点A的运动过程(力矩还是为零)。部分团队准确写出了相应的微分方程,并在比较特殊的情况下求解,如f=0的自由落体运动,圆周运动, 支撑力和重力的大小相等的运动,弹性杆满足胡克定律的运动,沿某一直线运动,设置沿抛物线运动等。第二小问需要在某特殊的f下模拟登上台阶的过程。提交该部分回答的团队,模拟结果都有一定的合理性。
B题:复杂约束下的排序问题
问题1只对满足矩阵表的小朋友进行排序,只有三种排序ADCBE, CADBE, ACDBE。它可以解析计算,也可用遍历计算,有向图拓扑排序,整数线性规划等。有向图拓扑排序和整数线性规划的方法值得鼓励。
问题2在问题1的排序基础上找目标函数最小的解ADCBE。它转化为分配问题,在3个排序的基础上找一个最优解,可使用整数线性规划。
问题3在问题1的排序基础上(排序表不同,小朋友个数变多)满足其它约束条件下最优的购买方案,由于总心情大于8,从而可解析地求出最优购买方案:2个红色秤、2个绿色秤和1个蓝色秤,花费224元,而且每个小朋友的心情也是确定的。即使在最优解下,也有三种情况的站秤方式,以及很多种小朋友排队顺序。求解方法可以是:解析方法,遍历计算,动态规划,整数线性规划。
问题4加上了两个约束,但是问题3的最优解都是满足这两个约束条件的。很多论文都准确的回答了这个问题。
问题5对一般的情况进行讨论。对矩阵表的合理性可用有向图有无闭环来判断,用算法判断矩阵表是否冲突,用Floyd算法求有向图的最短路径。对于第二个小问题,每篇论文给出了复杂度,取不同的小朋友个数得到CPU执行时间。如使用遍历算法和遗传算法分别求解,并说明了当n=12时遗传算法比遍历算法有很大优势。有些团队使用模拟退火算法执行说明n对执行时间影响不大。另外还有团队使用分支定界法、一般遍历算法,整数规划等验证对比了算法执行时间。
总结来说,该排序题目可用不少算法实现,但是整数规划和动态规划是值得提倡的,遍历算法也包含了两种方法。由于问题3中最优解是清楚的,所以这也为这些算法提供了验证的机会。提交团队们的论文表明这些算法都是可行的。
C题:期货高频交易收益率预测研究
金融数据相较于其他数据的最大特点之一,是其信噪比较低。一般在秒级频率对于下一个周期收益的预测,r方能高于5%的模型或者算法已经比较优秀。这种模型或算法需要专业团队不断地打磨和迭代。C题对于参赛团队的期待,首先是对金融数据建立正确的初步认识。 一部分团队对于数据认识有些偏差,很多反映在了过大的样本外r方上。原因可能是样本外测试时用到了样本内的数据,或者模型或算法有forward looking bias。
其次,因为赛题的解答是限时的,模型或算法的运用不需要特别尖端或新颖,基本用线性回归能做出一套比较规矩的解法。评委更看中的是在一定限制条件下(比如硬件、时间等)对于找到适合处理这类数据的方法。 从结果来看,一部分参赛团队运用了比较复杂的深度学习算法,但大多存在训练数据不足,或者泛化能力有待商榷的情况,而且基本较少涉及收敛、过拟合、超参数等的讨论。评委们能理解参赛选手想展现自己的知识储备的初衷,但在一个限时的赛题中选择如是解法略微显得有些在单纯“套”模型。
另外,在现实中一般都会做一个baseline的模型或算法,很多情况下线性回归模型是一个很好的基准,简单方便也比较鲁棒。当然,参赛团队勇于去挑战这类深度学习算法是值得肯定的。本题还有一个考验选手的地方在于对数据的处理能力。如果能在一定硬件条件下能熟练的使用Python或者其他的语言的包做数据处理,团队就能省下更多的时间打磨或尝试其他方法。这在现实的量化金融领域也是非常重要的一环。
问题1一个简单可能的方案就是单因子的线性回归。回归模型的评价除了题目给出的误差分析外,很重要的一点是看回归系数的t值和符号等等。即时r方很低,只要系数很显著,所对应的因子还是可有用武之地。
问题2是上一题的简单拓展。问题背景中给了不同档位成交顺序的例子,所以不同档位所蕴含的信息是不一样的。团队可根据档位的经济学含义适当构造一些强逻辑因子,但须注意样本外要小心验证。当然也可以全部丢进线性回归模型中,根据系数显著性保留或舍弃因子。相比问题1,此处r方应略有提升。若采用机器学习或深度模型,r方的提升会比线性更大。
问题3增加了一层时序的维度。关于动量(反转)的公式定义有很多,可以是一段时间内的收益,或收益除以波动率,或是其他的强逻辑。关于k的取值或取值范围,在线性框架下可以根据系数的显著性判断,比如可通过一张回归系数显著性对于k的变化的图来直观反映。当然不用线性模型的话样本外r方也是可取的。当k较小时一般会出现一些反转,或基本没有预测能力。k过大时预测能力也微乎其微。团队可选择一系列表现较为显著的k放进模型中作为因子。
问题4在前3题的基础上考察团队因子组合的思路。当然最简单的线性模型也是可取的。稍微复杂一些如boosting或者随机树也是很好的选择。这里需要考虑的因子的取舍和组合模型鲁棒性。这题偏总结性质,但完成度不是很高。当然也有一些团队对问题以外的金融数据特点做了探索,值得赞赏。